في الرياضيات ، يخصص التكامل أرقامًا للوظائف بطريقة تصف الإزاحة والمساحة والحجم والمفاهيم الأخرى التي تنشأ من خلال الجمع بين البيانات متناهية الصغر. تسمى عملية إيجاد التكاملات التكامل. إلى جانب التفاضل ، يعد التكامل عملية أساسية وأساسية لحساب التفاضل والتكامل ، ويعمل كأداة لحل المشكلات في الرياضيات والفيزياء التي تتضمن مساحة الشكل التعسفي وطول المنحنى وحجم المادة الصلبة ، من بين أمور أخرى.

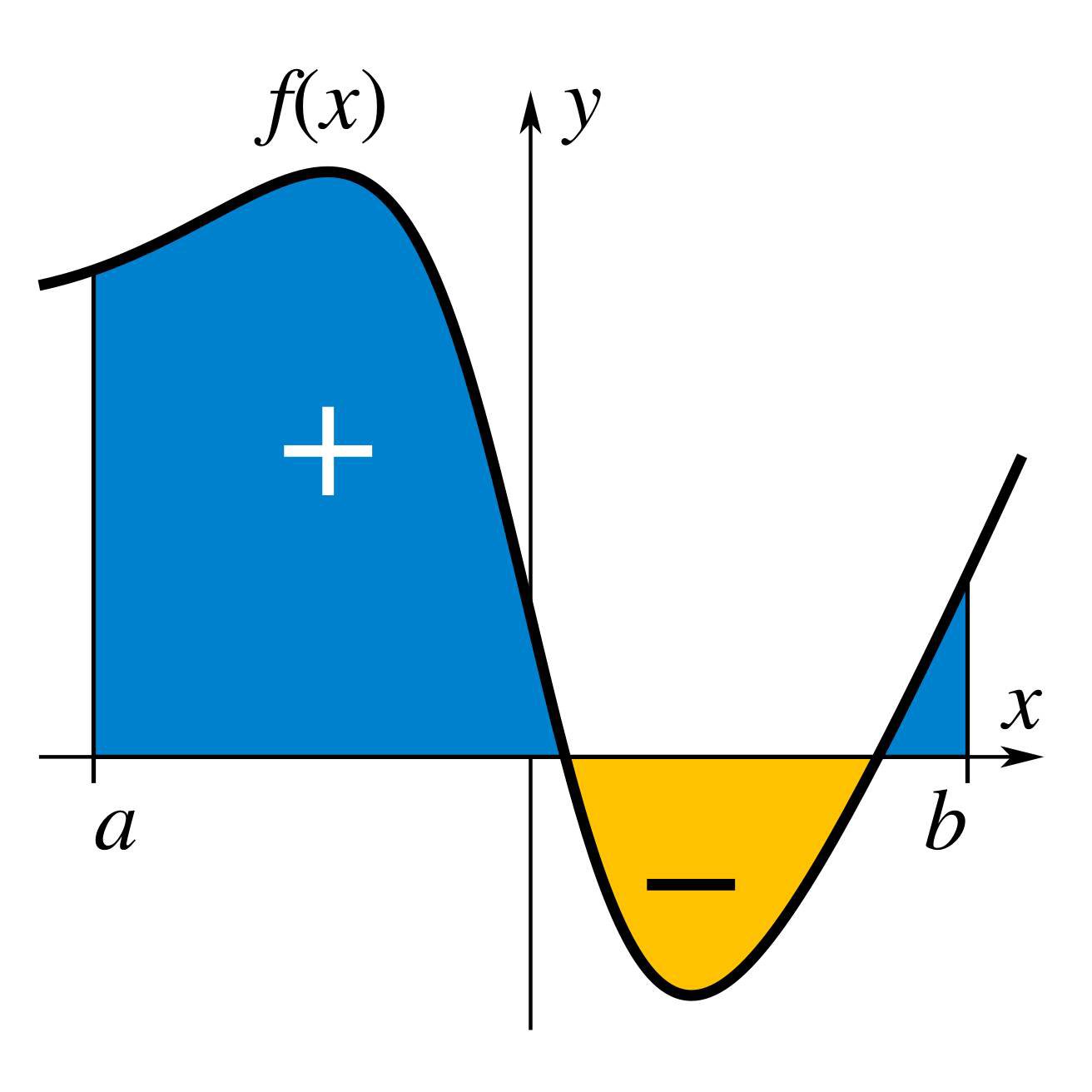
التكاملات التي تم تعدادها هنا هي تلك التي يطلق عليها التكاملات المحددة ، والتي يمكن تفسيرها على أنها المنطقة الموقعة من المنطقة في المستوى الذي يحده الرسم البياني لدالة معينة بين نقطتين في الخط الحقيقي. بشكل تقليدي ، تكون المساحات الموجودة فوق المحور الأفقي للمستوى موجبة بينما تكون المساحات أدناه سالبة. تشير التكاملات أيضًا إلى مفهوم المشتقة العكسية ، وهي وظيفة مشتقها هي الوظيفة المحددة. في هذه الحالة ، يطلق عليهم التكاملات غير المحددة. تتعلق النظرية الأساسية في التفاضل والتكامل بالتكاملات المحددة مع التفاضل وتوفر طريقة لحساب التكامل المحدد للدالة عندما تكون المشتقات العكسية معروفة.

على الرغم من أن طرق حساب المساحات والأحجام تعود إلى الرياضيات اليونانية القديمة ، إلا أن مبادئ التكامل صيغت بشكل مستقل من قبل إسحاق نيوتن وجوتفريد فيلهلم ليبنيز في أواخر القرن السابع عشر ، اللذين اعتقدا أن المنطقة الواقعة تحت المنحنى هي مجموع لا نهائي من المستطيلات ذات العرض اللامتناهي في الصغر. . قدم برنارد ريمان لاحقًا تعريفًا صارمًا للتكاملات ، والذي يعتمد على إجراء محدد يقارب مساحة المنطقة المنحنية عن طريق تقسيم المنطقة إلى ألواح عمودية رفيعة للغاية. في أوائل القرن العشرين ، عمم Henri Lebesgue صياغة ريمان من خلال تقديم ما يشار إليه الآن باسم Lebesgue لا يتجزأ. إنه أقوى من ريمان بمعنى أن فئة أوسع من الوظائف قابلة للتكامل في Lebesgue.

يمكن تعميم التكاملات اعتمادًا على نوع الوظيفة وكذلك المجال الذي يتم تنفيذ التكامل عليه. على سبيل المثال ، يتم تعريف تكامل الخط لوظائف متغيرين أو أكثر ، ويتم استبدال الفاصل الزمني للتكامل بمنحنى يربط بين نقطتي نهاية الفترة. في التكامل السطحي ، يتم استبدال المنحنى بقطعة من السطح في مساحة ثلاثية الأبعاد.

كان جوتفريد فيلهلم (فون) ليبنيز (1 يوليو 1646 [OS 21 يونيو] - 14 نوفمبر 1716) عالمًا متعدد الجوانب ألمانيًا نشطًا كعالم رياضيات وفيلسوف وعالم ودبلوماسي. إنه شخصية بارزة في كل من تاريخ الفلسفة وتاريخ الرياضيات. كتب أعمالًا في الفلسفة ، واللاهوت ، والأخلاق ، والسياسة ، والقانون ، والتاريخ ، وعلم اللغة. قدم لايبنيز أيضًا مساهمات كبيرة في الفيزياء والتكنولوجيا ، وتوقعت المفاهيم التي ظهرت بعد ذلك بكثير في نظرية الاحتمالات ، وعلم الأحياء ، والطب ، والجيولوجيا ، وعلم النفس ، واللغويات ، وعلوم الكمبيوتر. بالإضافة إلى ذلك ، ساهم في مجال علم المكتبات: أثناء عمله كمشرف على مكتبة Wolfenbüttel في ألمانيا ، ابتكر نظام فهرسة كان من شأنه أن يكون بمثابة دليل للعديد من المكتبات الكبرى في أوروبا. كانت مساهمات لايبنيز في هذه المجموعة الواسعة من الموضوعات مبعثرة في مختلف المجلات العلمية ، في عشرات الآلاف من الرسائل ، وفي المخطوطات غير المنشورة. كتب بعدة لغات ، في المقام الأول باللاتينية والفرنسية والألمانية ، ولكن أيضًا باللغات الإنجليزية والإيطالية والهولندية ، وكفيلسوف ، كان أحد أعظم ممثلي العقلانية والمثالية في القرن السابع عشر. كعالم رياضيات ، كان أعظم إنجازاته هو تطوير الأفكار الرئيسية لحساب التفاضل والتكامل ، بشكل مستقل عن التطورات المعاصرة لإسحاق نيوتن. لطالما فضلت الأعمال الرياضية تدوين ليبنيز باعتباره التعبير التقليدي لحساب التفاضل والتكامل ، ومع ذلك ، لم يكن قانون لايبنتز للاستمرارية وقانون التجانس المتسامي إلا في القرن العشرين ، حيث وجد صيغة رياضية متسقة عن طريق التحليل غير القياسي. كان أيضًا رائدًا في مجال الآلات الحاسبة الميكانيكية. أثناء عمله على إضافة الضرب والقسمة التلقائي إلى آلة حاسبة باسكال ، كان أول من وصف آلة حاسبة على شكل دولاب الهواء في عام 1685 واخترع عجلة لايبنيز ، المستخدمة في مقياس الحساب ، وهي أول آلة حاسبة ميكانيكية منتجة بكميات كبيرة. قام أيضًا بتحسين نظام الأرقام الثنائية ، وهو أساس جميع أجهزة الكمبيوتر الرقمية (الإلكترونية ، ذات الحالة الصلبة ، والمنطقية المنفصلة) تقريبًا ، بما في ذلك بنية Von Neumann ، وهي نموذج التصميم القياسي ، أو "بنية الكمبيوتر" ، المتبوعة من النصف الثاني من القرن العشرين والقرن الحادي والعشرين. يُطلق على لايبنيز لقب "مؤسس علوم الكمبيوتر". في الفلسفة واللاهوت ، يُعرف لايبنيز بتفاؤله ، أي استنتاجه أن عالمنا ، بالمعنى المؤهل ، هو أفضل عالم ممكن خلقه الله ، وجهة نظر أحيانًا يسخر منه مفكرون آخرون ، مثل فولتير في روايته الساخرة كانديد. كان لايبنيز ، جنبًا إلى جنب مع رينيه ديكارت وباروخ سبينوزا ، أحد أعظم ثلاثة عقلانيين حديثين في وقت مبكر. تستوعب فلسفته أيضًا عناصر من التقليد المدرسي ، ولا سيما الافتراض بأن بعض المعرفة الموضوعية للواقع يمكن تحقيقها من خلال الاستدلال من المبادئ الأولى أو التعريفات السابقة. توقع عمل لايبنيز المنطق الحديث ولا يزال يؤثر على الفلسفة التحليلية المعاصرة ، مثل الاستخدام المعتمد لمصطلح "العالم الممكن" لتعريف المفاهيم النمطية.