En mathématiques, une intégrale attribue des nombres aux fonctions d'une manière qui décrit le déplacement, la surface, le volume et d'autres concepts qui surviennent en combinant des données infinitésimales. Le processus de recherche d'intégrales s'appelle l'intégration. Avec la différenciation, l'intégration est une opération fondamentale et essentielle du calcul et sert d'outil pour résoudre des problèmes de mathématiques et de physique impliquant l'aire d'une forme arbitraire, la longueur d'une courbe et le volume d'un solide, entre autres.

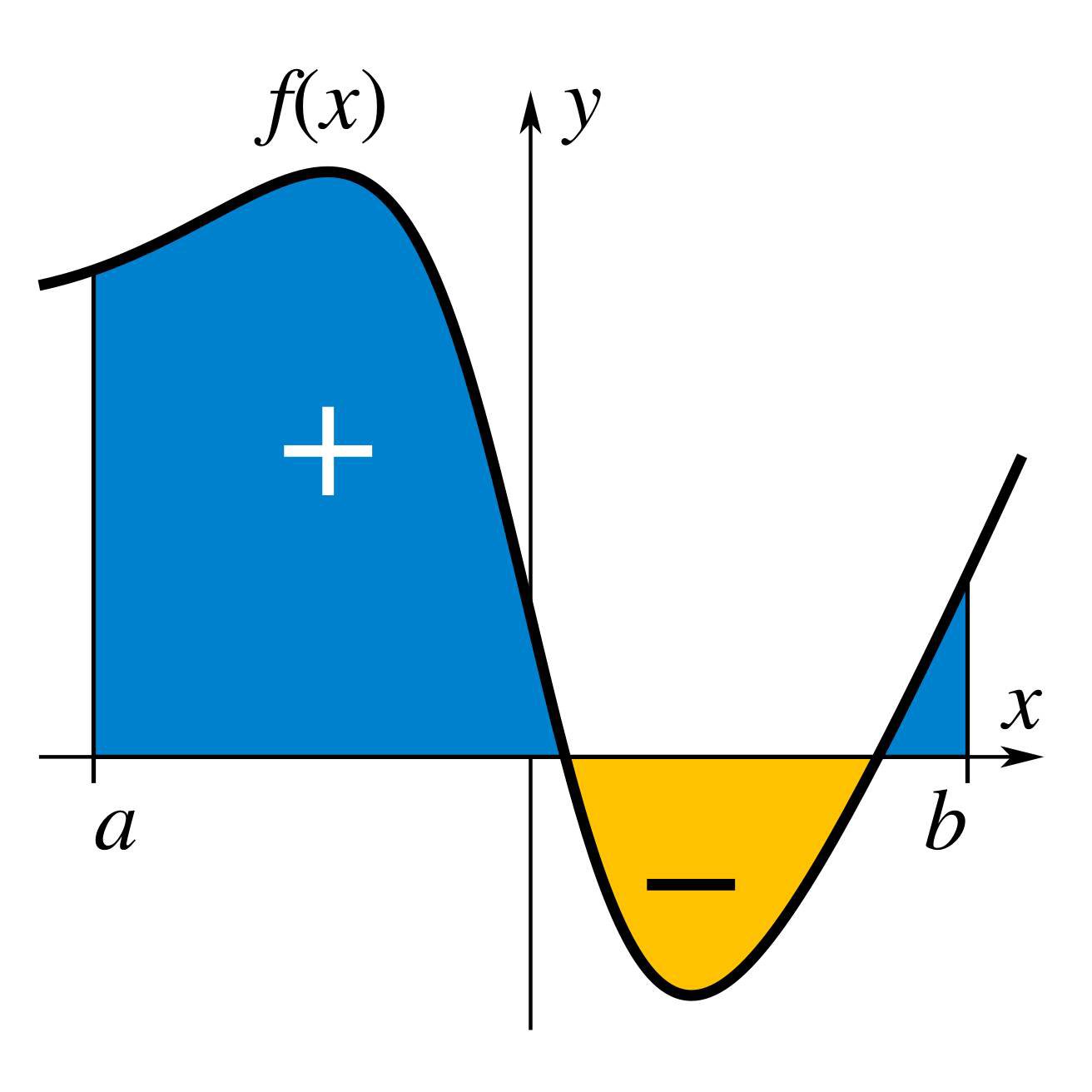
Les intégrales énumérées ici sont celles appelées intégrales définies, qui peuvent être interprétées comme la zone signée de la région dans le plan qui est délimitée par le graphique d'une fonction donnée entre deux points de la ligne réelle. Classiquement, les zones au-dessus de l'axe horizontal du plan sont positives tandis que les zones en dessous sont négatives. Les intégrales font également référence au concept de primitive, une fonction dont la dérivée est la fonction donnée. Dans ce cas, elles sont appelées intégrales indéfinies. Le théorème fondamental du calcul relie les intégrales définies à la différenciation et fournit une méthode pour calculer l'intégrale définie d'une fonction lorsque sa primitive est connue.

Bien que les méthodes de calcul des aires et des volumes datent des mathématiques de la Grèce antique, les principes d'intégration ont été formulés indépendamment par Isaac Newton et Gottfried Wilhelm Leibniz à la fin du XVIIe siècle, qui considéraient l'aire sous une courbe comme une somme infinie de rectangles de largeur infinitésimale. . Bernhard Riemann a donné plus tard une définition rigoureuse des intégrales, qui est basée sur une procédure de limitation qui se rapproche de la surface d'une région curviligne en divisant la région en dalles verticales infiniment minces. Au début du XXe siècle, Henri Lebesgue a généralisé la formulation de Riemann en introduisant ce que l'on appelle maintenant l' intégrale de Lebesgue ; il est plus robuste que celui de Riemann en ce sens qu'une classe plus large de fonctions est intégrable à Lebesgue.

Les intégrales peuvent être généralisées en fonction du type de fonction ainsi que du domaine sur lequel l'intégration est effectuée. Par exemple, une intégrale linéaire est définie pour les fonctions de deux variables ou plus, et l'intervalle d'intégration est remplacé par une courbe reliant les deux extrémités de l'intervalle. Dans une intégrale de surface, la courbe est remplacée par un morceau de surface dans un espace tridimensionnel.

Gottfried Wilhelm (von) Leibniz (1er juillet 1646 [ OS 21 juin] - 14 novembre 1716) était un mathématicien allemand actif en tant que mathématicien, philosophe, scientifique et diplomate. Il est une figure marquante de l'histoire de la philosophie et de l'histoire des mathématiques. Il a écrit des ouvrages sur la philosophie, la théologie, l'éthique, la politique, le droit, l'histoire et la philologie. Leibniz a également apporté des contributions majeures à la physique et à la technologie, et a anticipé des notions qui sont apparues beaucoup plus tard dans la théorie des probabilités, la biologie, la médecine, la géologie, la psychologie, la linguistique et l'informatique. En outre, il a contribué au domaine de la bibliothéconomie : alors qu'il était surveillant de la bibliothèque de Wolfenbüttel en Allemagne, il a conçu un système de catalogage qui aurait servi de guide à de nombreuses bibliothèques parmi les plus grandes d'Europe. Les contributions de Leibniz à ce vaste éventail de sujets ont été dispersées dans diverses revues savantes, dans des dizaines de milliers de lettres et dans des manuscrits non publiés. Il écrivit en plusieurs langues, principalement en latin, français et allemand, mais aussi en anglais, italien et néerlandais. En tant que philosophe, il fut l'un des plus grands représentants du rationalisme et de l'idéalisme du XVIIe siècle. En tant que mathématicien, sa plus grande réussite a été le développement des principales idées du calcul différentiel et intégral, indépendamment des développements contemporains d'Isaac Newton. Les travaux mathématiques ont toujours favorisé la notation de Leibniz comme expression conventionnelle du calcul. Cependant, ce n'est qu'au XXe siècle que la loi de continuité et la loi transcendantale d'homogénéité de Leibniz ont trouvé une formulation mathématique cohérente au moyen d'une analyse non standard. Il a également été un pionnier dans le domaine des calculatrices mécaniques. Tout en travaillant sur l'ajout de la multiplication et de la division automatiques à la calculatrice de Pascal, il fut le premier à décrire une calculatrice à moulinet en 1685 et inventa la roue de Leibniz, utilisée dans l'arithmomètre, la première calculatrice mécanique produite en série. Il a également affiné le système de numération binaire, qui est à la base de presque tous les ordinateurs numériques (électroniques, à semi-conducteurs, à logique discrète), y compris l'architecture Von Neumann, qui est le paradigme de conception standard, ou "architecture informatique", suivie depuis le seconde moitié du 20ème siècle, et dans le 21ème. Leibniz a été appelé le "fondateur de l'informatique". En philosophie et en théologie, Leibniz est surtout connu pour son optimisme, c'est-à-dire sa conclusion que notre monde est, dans un sens qualifié, le meilleur monde possible que Dieu aurait pu créer, une vue parfois ridiculisé par d'autres penseurs, comme Voltaire dans son roman satirique Candide. Leibniz, avec René Descartes et Baruch Spinoza, était l'un des trois grands rationalistes de la première modernité. Sa philosophie assimile également des éléments de la tradition scolastique, notamment l'hypothèse selon laquelle une certaine connaissance substantielle de la réalité peut être obtenue en raisonnant à partir de principes premiers ou de définitions antérieures. Le travail de Leibniz a anticipé la logique moderne et influence toujours la philosophie analytique contemporaine, comme son utilisation adoptée du terme «monde possible» pour définir les notions modales.