В математике интеграл присваивает числа функциям таким образом, который описывает смещение, площадь, объем и другие понятия, возникающие при объединении бесконечно малых данных. Процесс нахождения интегралов называется интегрированием. Наряду с дифференцированием интегрирование является фундаментальной, существенной операцией исчисления и служит инструментом для решения задач в математике и физике, связанных, среди прочего, с площадью произвольной формы, длиной кривой и объемом твердого тела.

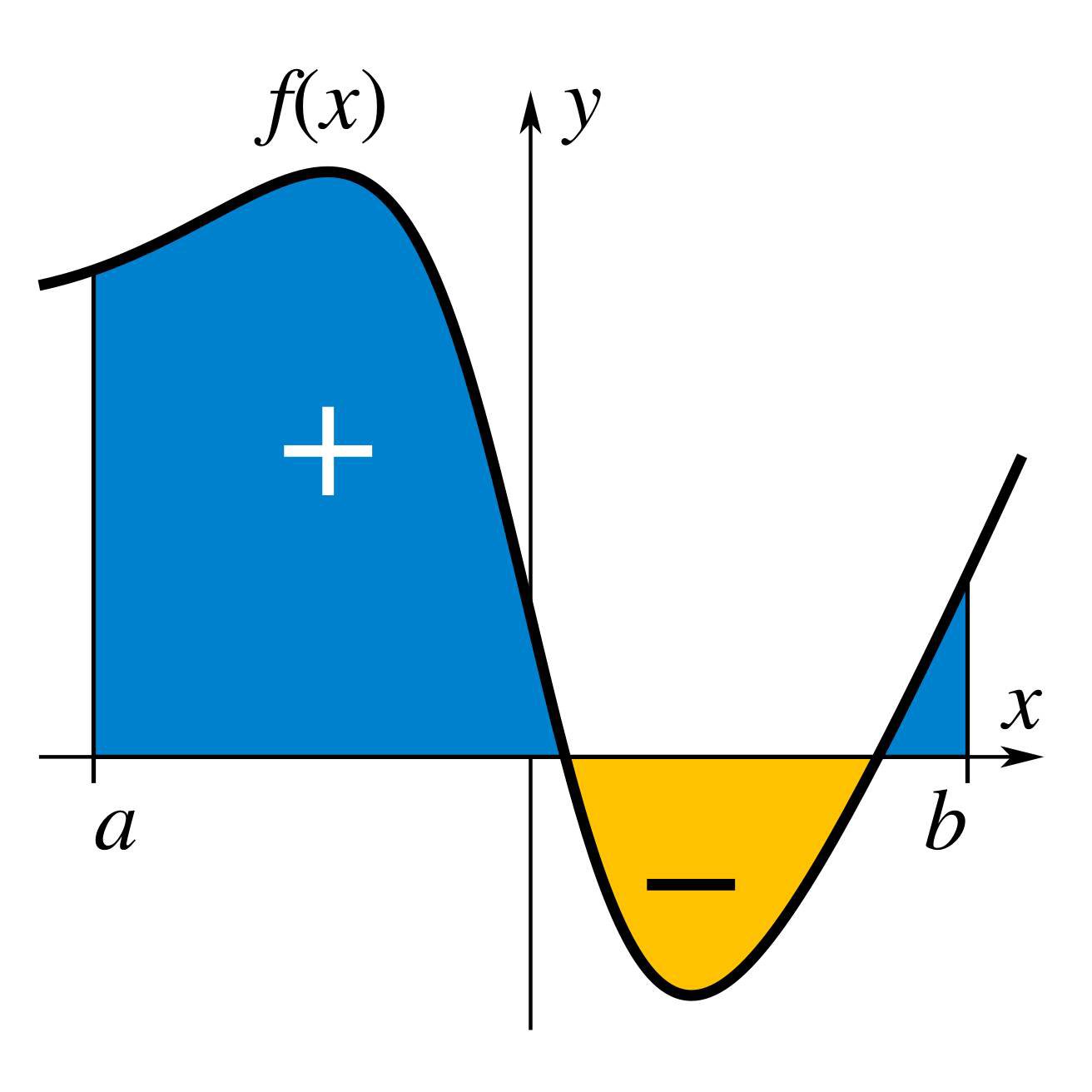
Перечисленные здесь интегралы называются определенными интегралами, которые можно интерпретировать как площадь со знаком области на плоскости, ограниченной графиком данной функции между двумя точками на прямой. Обычно области выше горизонтальной оси плоскости являются положительными, а области ниже - отрицательными. Интегралы также относятся к понятию первообразной функции, производной которой является данная функция. В этом случае их называют неопределенными интегралами. Основная теорема исчисления связывает определенные интегралы с дифференцированием и дает метод вычисления определенного интеграла функции, когда известна ее первообразная.

Хотя методы вычисления площадей и объемов восходят к древнегреческой математике, принципы интегрирования были сформулированы независимо Исааком Ньютоном и Готфридом Вильгельмом Лейбницем в конце 17 века, которые представляли площадь под кривой как бесконечную сумму прямоугольников бесконечно малой ширины. . Позже Бернхард Риман дал строгое определение интегралов, основанное на предельной процедуре, которая аппроксимирует площадь криволинейной области, разбивая область на бесконечно малые вертикальные пластины. В начале 20 века Анри Лебег обобщил формулировку Римана, введя то, что сейчас называется интегралом Лебега; он более надежен, чем римановский, в том смысле, что более широкий класс функций интегрируем по Лебегу.

Интегралы могут быть обобщены в зависимости от типа функции, а также области, по которой выполняется интегрирование. Например, линейный интеграл определяется для функций двух или более переменных, а интервал интегрирования заменяется кривой, соединяющей две конечные точки интервала. В поверхностном интеграле кривая заменяется частью поверхности в трехмерном пространстве.

Готфрид Вильгельм (фон) Лейбниц (1 июля 1646 г. [ OS 21 июня] - 14 ноября 1716 г.) был немецким эрудитом, работавшим как математик, философ, ученый и дипломат. Он видная фигура как в истории философии, так и в истории математики. Он написал работы по философии, теологии, этике, политике, праву, истории и филологии. Лейбниц также внес большой вклад в физику и технику и предвосхитил идеи, появившиеся гораздо позже в теории вероятностей, биологии, медицине, геологии, психологии, лингвистике и компьютерных науках. Кроме того, он внес свой вклад в область библиотечного дела: работая надзирателем библиотеки Вольфенбюттеля в Германии, он разработал систему каталогизации, которая послужила бы руководством для многих крупнейших библиотек Европы. Вклад Лейбница в этот широкий круг вопросов был разбросан по разным научным журналам, десяткам тысяч писем и неопубликованным рукописям. Он писал на нескольких языках, прежде всего на латыни, французском и немецком, а также на английском, итальянском и голландском языках. Как философ он был одним из величайших представителей рационализма и идеализма 17 века. Его величайшим достижением как математика было развитие основных идей дифференциального и интегрального исчисления независимо от современных разработок Исаака Ньютона. Математические работы последовательно отдавали предпочтение обозначениям Лейбница как общепринятому выражению исчисления. Однако только в 20 веке закон непрерывности Лейбница и трансцендентный закон однородности нашли непротиворечивую математическую формулировку с помощью нестандартного анализа. Он также был пионером в области механических калькуляторов. Работая над добавлением автоматического умножения и деления к калькулятору Паскаля, он первым описал вертушку калькулятора в 1685 году и изобрел колесо Лейбница, использовавшееся в арифмометре, первом массовом механическом калькуляторе. Он также усовершенствовал двоичную систему счисления, которая является основой почти всех цифровых (электронных, твердотельных, с дискретной логикой) компьютеров, включая архитектуру фон Неймана, которая является стандартной парадигмой проектирования, или «компьютерной архитектурой». второй половине 20-го века и в 21-м. Лейбница называют «основателем компьютерных наук». В философии и богословии Лейбниц наиболее известен своим оптимизмом, т. е. его выводом о том, что наш мир, в определенном смысле, является лучшим из возможных миров, которые мог создать Бог. иногда высмеивается другими мыслителями, такими как Вольтер в его сатирической новелле «Кандид». Лейбниц, наряду с Рене Декартом и Барухом Спинозой, был одним из трех великих рационалистов раннего Нового времени. Его философия также ассимилирует элементы схоластической традиции, особенно предположение о том, что некоторое существенное знание реальности может быть достигнуто путем рассуждений на основе первых принципов или предварительных определений. Работа Лейбница предвосхитила современную логику и до сих пор влияет на современную аналитическую философию, например, в принятом ею использовании термина «возможный мир» для определения модальных понятий.