在数学中，积分以描述位移、面积、体积和其他通过组合无穷小数据产生的概念的方式将数字分配给函数。求积分的过程称为积分。与微分一样，积分是微积分的基本基本运算，可作为解决数学和物理问题的工具，涉及任意形状的面积、曲线的长度和实体的体积等。

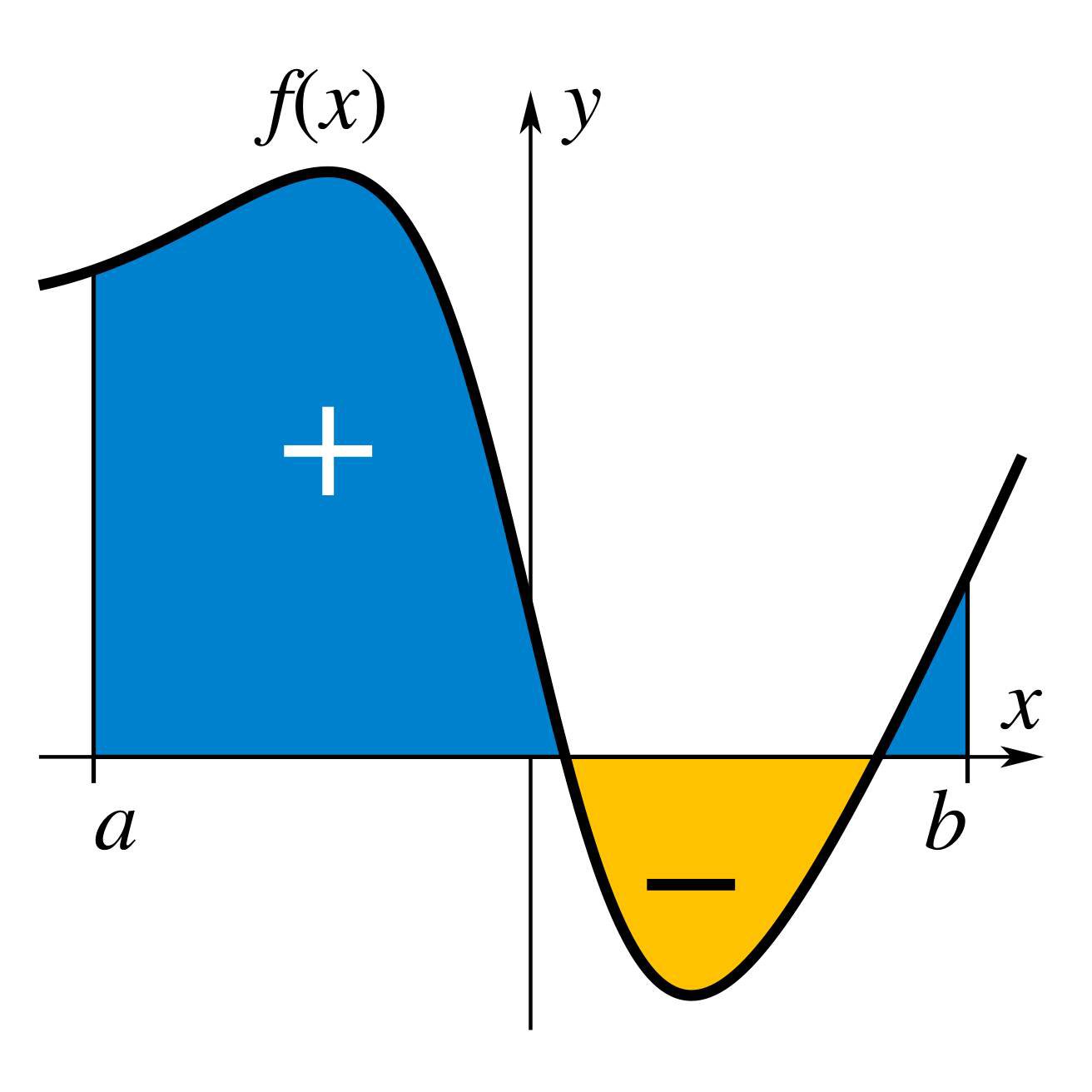
这里列举的积分被称​​为定积分，可以解释为平面中区域的有符号面积，该区域由实线中两点之间的给定函数的图形界定。通常，平面水平轴上方的区域为正，而下方的区域为负。积分也指反导数的概念，即导数是给定函数的函数。在这种情况下，它们被称为不定积分。微积分的基本定理将定积分与微分联系起来，并提供了一种在已知反导数时计算函数定积分的方法。

虽然计算面积和体积的方法可以追溯到古希腊数学，但积分原理是由艾萨克牛顿和戈特弗里德威廉莱布尼茨在 17 世纪后期独立制定的，他们认为曲线下面积是无限小宽度矩形的无限总和. Bernhard Riemann 后来给出了积分的严格定义，它基于一个限制程序，该程序通过将曲线区域分解为无限薄的垂直板来近似该区域的面积。在 20 世纪初，Henri Lebesgue 通过引入现在被称为 Lebesgue 积分的东西推广了黎曼的公式。在更广泛的函数类是勒贝格可积的意义上，它比黎曼的更健壮。

积分可以根据函数的类型以及执行积分的域进行泛化。例如，为两个或多个变量的函数定义线积分，积分区间由连接区间两个端点的曲线代替。在曲面积分中，曲线由三维空间中的一块曲面代替。

戈特弗里德·威廉 (von) Leibniz（1646 年 7 月 1 日 [O.S. 6 月 21 日] – 1716 年 11 月 14 日）是一位活跃于数学家、哲学家、科学家和外交官的德国博学家。他是哲学史上和数学史上的杰出人物。他的著作涉及哲学、神学、伦理学、政治学、法律、历史和语言学。莱布尼茨还对物理学和技术做出了重大贡献，并预见了后来在概率论、生物学、医学、地质学、心理学、语言学和计算机科学中出现的概念。此外，他还为图书馆学领域做出了贡献：在担任德国沃尔芬比特图书馆馆长期间，他设计了一个编目系统，该系统可以作为欧洲许多最大图书馆的指南。莱布尼茨对这一浩瀚主题的贡献分散在各种学术期刊、数以万计的信件和未发表的手稿中。他用多种语言写作，主要是拉丁语、法语和德语，但也有英语、意大利语和荷兰语。作为哲学家，他是 17 世纪理性主义和唯心主义的最伟大代表之一。作为一名数学家，他最大的成就是独立于艾萨克·牛顿同时期的发展，发展了微积分和积分的主要思想。数学著作一直青睐莱布尼茨符号作为微积分的常规表达方式。然而，直到20世纪，莱布尼茨的连续性定律和先验齐性定律才通过非标准分析找到了一致的数学公式。他还是机械计算器领域的先驱。在为帕斯卡的计算器添加自动乘法和除法时，他在 1685 年首次描述了风车计算器，并发明了莱布尼茨轮，用于算术计，这是第一台大规模生产的机械计算器。他还改进了二进制数系统，它是几乎所有数字（电子、固态、离散逻辑）计算机的基础，包括标准设计范式或“计算机架构”的冯诺依曼架构，从20世纪下半叶，进入21世纪。莱布尼茨被称为“计算机科学的创始人”。在哲学和神学中，莱布尼茨最出名的是他的乐观主义，即他的结论是，我们的世界在一定意义上是上帝可能创造的最好的世界，一种观点有时被其他思想家讽刺，例如伏尔泰在他的讽刺中篇小说《老实人》中。莱布尼茨与勒内·笛卡尔和巴鲁克·斯宾诺莎一起，是早期现代三大理性主义者之一。他的哲学也吸收了学术传统的元素，特别是假设可以通过从第一原理或先前定义进行推理来获得对现实的一些实质性知识。莱布尼茨的工作预见了现代逻辑，并且仍然影响着当代分析哲学，例如它采用了“可能世界”一词来定义模态概念。